FoxCalculators - অনলাইনে বিনামূল্যে ক্যালকুলেটর!

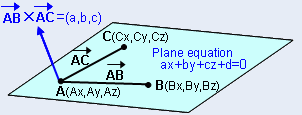
তিনটি পয়েন্ট A (x _{1 , y 1 , z 1 ), B (x 2 , y <সাব> 2 , z 2 ) এবং c (x 3 , y 3 , z 3 ) একটি সমতল উপর মিথ্যা, তারপর সমতল সমীকরণ নিম্নলিখিত সূত্র ব্যবহার করে পাওয়া যাবে}

<টেবিল align = "কেন্দ্র" শৈলী = "সীমানা ধসে: পতন;">

.

.

x - x ₁

y - y ₁

z - z ₁

= 0

x _{2 - x 1}

y _{2 - Y 1}

z _{2 - z 1}

x _{3 - x 1}

Y _{3 - Y 1}

z _{3 - z 1}

অথবা একটি (AX, AY, AZ), B (BX, দ্বারা, BZ), C (CX, CY, CZ), সমতল সমীকরণটি + + cz + d = 0 দ্বারা + + + + +

কোথায়,

A = (BY-AY) (CZ-AZ) - (CY-AY) (BZ-AZ)

বি = (BZ-AZ) (CX-AX) - (CZ-AZ) (BX-AX)

সি = (বিএক্স-এক্স) (সিএ-আই) - (সিএক্স-এক্স) (বাই-আই)

ডি = - (AAX + বে + CAZ)।

তিনটি কোঅর্ডিনেটস সহ কার্টেসিয়ান সমীকরণ সমীকরণ গণনা এখানে সহজ করা হয়।